DZIELENIE
To w matematyce operacja zdefiniowana w dowolnym ciele jako:
 , dla
, dla 
Ponieważ dzielenie defiujemy jako mnożenie przez odwrotność, nie można dzielić przez 0, gdyż nie istnieje liczba odwrotna do 0, ze względu na mnożenie (tzn. nie istnieje liczba, która, pomnożona przez 0, da nam element neutralny mnożenia, czyli 1). gdzie  to element odwrotny do b.
to element odwrotny do b.
W działaniu tym występują dwa operandy nazywające się dzielną i dzielnikiem. Wynik dzielenia nazywany jest ilorazem.
Do zapisu operacji dzielenia używa się alternatywnie symboli  .
.
Podstawowe algorytmy dzielenia
W ciele liczb rzeczywistych
Przykładem będzie dzielenie  , co daje w wyniku
, co daje w wyniku . Gdy
. Gdy  ,
,  jest nieokreślone (zob. artykuł dzielenie przez zero). Gdy
jest nieokreślone (zob. artykuł dzielenie przez zero). Gdy  jest równe podstawie systemu pozycyjnego podniesionej do potęgi
jest równe podstawie systemu pozycyjnego podniesionej do potęgi  , to
, to  równe jest
równe jest  przesuniętemu względem przecinka w prawo o
przesuniętemu względem przecinka w prawo o  (dla dowolnego systemu pozycyjnego).
(dla dowolnego systemu pozycyjnego).
W ciele 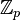 (całkowitych reszt modulo liczba pierwsza p)
(całkowitych reszt modulo liczba pierwsza p)
Znajdujemy najmniejszą liczbę naturalną  , taką że:
, taką że:
Wtedy:





